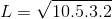Wartawankampung.com - Apakah kalian sudah mengetahui bagaimana bentuk segitiga? Atau kalian juga sudah mengetahui rumus segitiga yang digunakan untuk menghitung luas bangun datar tersebut?
Bagi kamu yang belum tahu, Segitiga adalah sebuah bangun datar yang memiliki tiga buah sisi. Setiap sisi itu kemudian bertemu dan membentuk sebuah bangun datar yang disebut segitiga. Ini dia gambar bangun datar segitiga.
Sebelum masuk ke dalam pembahasan rumus segitiga, ada baiknya jika kamu mengenal apa itu segitiga terlebih dahulu? Segitiga merupakan salah satu bangun datar yang dibatasi oleh tiga buah ruas garis, dimana tiap dua buah garis selalu berpotongan dalam satu titik. Ruas-ruas yang terdapat dalam segitiga sering dikenal dengan sisi-sisi segitiga. Atau yang sering dilambangkan dengan tanda
Menurut euclid, apabila dijumlahkan, keseluruhan sudut segitiga itu akan menghasilkan nilai sebesar 1800. Denagn demikian, kita bisa menghitung salah satu sudut segitiga jika sudut-sudut yang lain sudah diketahui.
Tulisan ini juga akan membahas secara lengkap mengenai rumus-rumus segitiga. Selain itu, tulisan ini juga akan memberikan beberapa contoh soal agar kamu bisa memahami bagaimana cara menghitung luas dan keliling segitiga.
Jenis-jenis Segitiga
Umumnya segitiga terdiri dari beberapa jenis. Jenis-jenis segitiga ini diketahui berdasarkan panjang setiap sisinya yang membentuk segitiga tersebut. segitiga dibagi menjadi tiga jenis, ketiga jenis tersebut antara lain adalah:
#Segitiga sama sisi
Segitiga ini merupakan segitiga yang memiliki panjang setiap sisinya sama dan masing-masing sudut yang ada pada segitiga sudut tersebut sama besar yaitu 600. Segitiga jenis ini umumnya biasanya akan terlihat seimbang dan kokoh.
Segitiga sama kaki
Segitiga ini adalah segita yang memiliki dua sisi yang sama panjang. Dengan demikian, secara otomatis segitiga ini juga memiliki 2 suduh dengan besar yang sama persis.
#Segitiga sembarang
Segitiga ini sangat berbeda dengan segitiga sama sisi maupun segitiga sama kaki. Segitiga sembarang adalah segitiga yang dibentuk dari 3 sisi yang memiliki panjang yang sisi yang berbeda-beda. Oleh karena itu, besar sudut setiap sudut yang ada pada segitiga jenis ini juga berbeda-beda.
Agar kamu dapat lebih mudah memahami dan membedakan ketiga jenis segitiga tersebut, coba lihat gambar dibawah ini.
Seperti yang telah kita ketahui segitiga merupakan suatu bangun datar yang dibatasi oleh tiga buah sisi dan mempunyai tiga titik sudut.
Jumlah ketiga titik sudut segitiga adalah 180°, sehingga apabila besar salah satu atau kedua titik sudutnya diketahui kita dapat mencari besar titik sudut yang lainnya.
Contoh soal:
Perhatikan gambar berikut!
Diketahui ∠A = 45°, ∠B = 60°, tentukan besar sudut C!
180° = ∠A+∠B+∠C
180° = 45°+60°+∠C
∠C = 180° - (45°+60°)
∠C = 180° - 105°
∠C = 75°
Jenis-jenis segitiga:
1. berdasarkan panjang sisinya
2. berdasarkan besar sudutnya
Luas dan Keliling Segitiga
Luas
Luas adalah 1/2 dikali panjang alas dan tingginya.
Keliling
keliling adalah jumlah panjang sisi-sisi yang membatasi bidang datar tersebut.
Untuk segitiga sama sisi (misalnya panjang sisi-sisinya kita sebut a) luas dan kelilingnya dapat juga kita cari dengan menggunakan rumus;
Contoh soal:
Tentukan luas dan keliling pada segitiga sama kaki berikut, jika diketahui PR = 12cm, QS = 8cm, dan QR = 10cm!
Pembahasan:
Pada segitiga diatas PR = alas segitiga, dan QS = tingginya.
Keliling = sisi1+sisi2+sisi3 (karena segitiga diatas sama kaki maka PQ = QR = 10cm)
Keliling = 12+10+10
=36 cm
Mencari luas segitiga dengan Teorema Heron
Teorema Heron biasanya digunakan untuk mencari luas segitiga sembarang, misalnya a, b, dan c adalah ketiga sisi segitiga maka luas segitiga tersebut adalah:
dimana s = semiperimeter yaitu 1/2 keliling, atau
baca juga: Contoh Soal dan Pembahasan Segitiga
Contoh soal:
Diketahui sebuah segitiga sembarang dengan panjang masing-masing sisinya yaitu 5 cm, 7 cm, dan 8 cm. tentukan luas dari segitiga tersebut!
Pembahasan:
hitung nilai semiperimeternya:
Luas segitiga:
Teorema Phytagoras
Teorema Phytagoras adalah teorema yang menunjukan hubungan setiap panjang sisi-sisi pada segitiga siku-siku. Teorema ini hanya berlaku untuk segitiga siku-siku, yaitu segitiga yang besar salah satu sudutnya adalah 90°.
Teorema Phytagoras menyatakan bahwa 
dengan titik C sebagai sudut siku-siku.
dengan titik C sebagai sudut siku-siku.Agar lebih jelas silakan perhatikan gambar berikut:
Jika ada tiga buah bilangan a, b, dan c yang memenuhi persamaan Phytagoras diatas maka ketiga bilangan tersebut disebut bilangan Triple Phytagoras. (penjelasan lebih lanjut mengenai triple phytagoras silakan baca: Triple Phytagoras)
Contoh soal:
Sebuah segitiga, siku-siku dititik C. Diketahui panjang AB = 25cm, BC = 15cm. Berapakah panjang AC?
Pembahasan:
berdasarkan teorema phytagoras ;
sehingga,
Lingkaran dalam dan Luar Segitiga
Lingkaran dalam segitiga
Lingkaran dalam segitiga adalah suatu lingkaran yang berada didalam segitiga serta menyinggung ketiga sisi segitiga tersebut. Jari-jari lingkaran dalam segitiga dirumuskan sebagai berikut:
dimana r = jari-jari lingkaran dalam segitiga
L=luas segitiga
s=1/2 keliling segitiga
Lingkaran luar segitiga
Lingkaran luar segitiga adalah lingkaran yang berada diluar sigitiga serta keliling segitiga tersebut menyinggung perpotongan tiga garis segitiga. Jari-jari lingkaran luar segitiga dirumuskan sebagai berikut:
Lingkaran luar segitiga adalah lingkaran yang berada diluar sigitiga serta keliling segitiga tersebut menyinggung perpotongan tiga garis segitiga. Jari-jari lingkaran luar segitiga dirumuskan sebagai berikut:
R = jari-jari lingkaran luar segitiga
a, b, dan c = 3 sisi segitiga
L = luas segitiga
L = luas segitiga
Perhatikan rumus lingkaran dalam maupun lingkaran luar segitiga diatas, masing-masing terdapat L (Luas segitiga), luas segitiga disini dapat kita cari dengan mengetahui jenis segitiga yang ada pada lingkaran dalam maupun lingkaran luar segitiga tersebut. (penjelasan lebih lanjut mengenai lingkaran dalam dan lingkaran luar segitiga akan saya buat pada artikel selanjutnya).
Contoh soal:
Tentukan jari-jari lingkaran dalam segitiga berikut ini jika diketahui panjang AB = 16cm, BC = 12cm, dan AC = 20cm!
Pembahasan:
kemudian hitung luas segitiga:
sehingga nilai jari-jarinya adalah:
Mohon maaf jika ada kata ataupun perhitungan yang salah dalam postingan diatas.